最大公因數 (GCD)

最大公因數 (GCD)，是能夠整除兩個正整數 a 和 b 的最大數值。

例子：

對於 a = 12，b = 8，我們可以計算它們的因數：

• a 的因數：{1, 2, 3, 4, 6, 12}
• b 的因數：{1, 2, 4, 8}

比較這兩組因數，我們發現 gcd(a, b) = 4。

假設我們取 a = 11，b = 17。由於這兩個數都是質數，質數的因數只有它自己和 1，因此 gcd(a,b)=1。

所以對於任意兩個整數 a 和 b，如果 gcd(a, b) = 1 ，那麼 a 和 b 就是互質數。

• 如果 a 和 b 都是質數，那麼它們也是互質的。
• 如果 a 是質數，且 b < a，那麼 a 和 b 也必定是互質的。

計算 GCD 的方法

要如何計算出 GCD 呢？有兩種常見的方法：

1. 質因數分解法：

   • 將 a 和 b 分解為質因數，然後取兩者共有質因數的最低次方。
   • 雖然這個方法較為直觀，但對於大數的計算效率不高。

2. 輾轉相除法、歐幾里得算法 (Euclid's Algorithm)：

   • 這是一個基於遞迴減少問題規模的高效算法，通過反覆求餘來逐步縮小範圍，最終求得 GCD。
   • 這個方法較有效率。

歐幾里得算法

核心概念：
不斷地用較大的數去除以較小的數，直到餘數為 0，這時候的除數就是最大公因數。

具體步驟

1. 先取兩個數 a 和 b（假設 a>b ）。
2. 把 a 除以 b，得到一個餘數 r 。
3. 如果 r = 0，那麼 b 就是 a 和 b 的最大公因數。
4. 如果 r != 0，就把 b 當作新的 a，把餘數 r 當作新的 b，重複前面的步驟，直到餘數為 0。

而用公式表示的話則是: ** gcd(a,b)=gcd(b,a mod b)**
其中，a mod b = a 除以 b 得到的餘數 r

簡單範例

假設我們要找 108 和 16 的最大公因數，按照歐幾里得算法的步驟來做：

• 先用 108 除以 16，得到餘數 12。
• 現在，我們用 16 除以 12，得到餘數 4。
• 接著，用 12 除以 4，得到餘數 0。
• 因為餘數是 0，所以 4 就是 108 和 16 的最大公因數。
• 手算筆記:

Modular-GCD

https://cryptohack.org/courses/modular/gcd/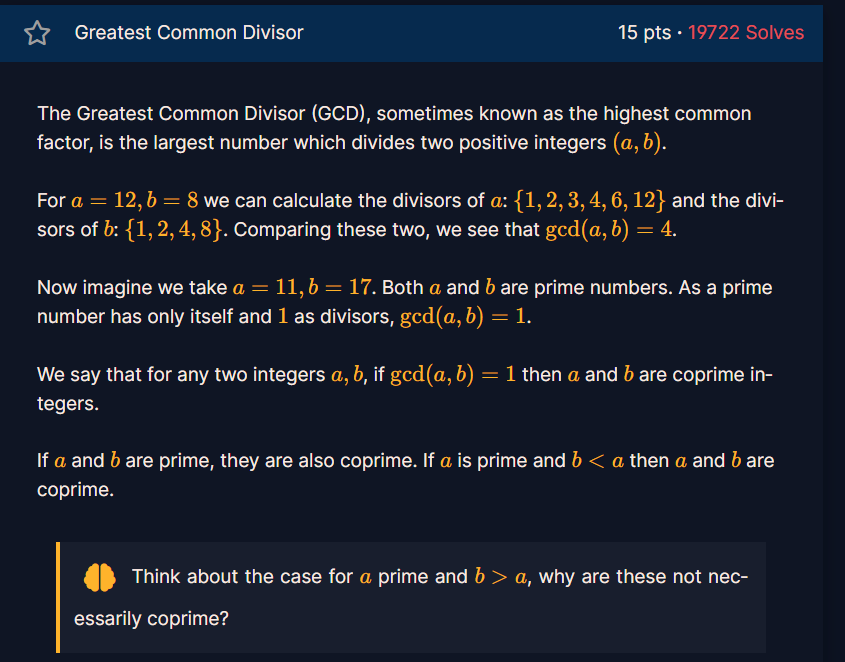

題意:

題目要我們找出 66528 和 52920 的最大公因數

程式碼與簡要註解:

解法一:寫一個gcd的函式

def GCD(a, b):
    # 如果 b > a，則交換 a 和 b 的數值
    if a < b:
        c = b
        b = a
        a = c
        
    # 如果 b 等於 0，則 a 是最大公因數，返回 a
    if b == 0:
        return a
    
    # 如果 b 不等於 0，則遞歸地尋找最大公因數，返回 GCD(b, a % b)
    else:
        return GCD(b, a % b)

print(GCD(66528, 52920))

＞1512

解法二:直接套函示庫

import math
print(math.gcd(66528,52920))

＞1512

EGCD介紹

擴展歐幾里得算法（Extended Euclidean Algorithm, EGCD）

• 是歐幾里得算法（Euclidean Algorithm）的延伸
• EGCD 除了求出最大公因數外，還能找到一組整數解 x 和 y，滿足：

ax + by = gcd(a, b)

而這個等式稱為貝祖等式（Bézout's identity）。

• 不一定只會有一組x和y成立此等式
• 手算筆記
  

Modular-EGCD

https://cryptohack.org/courses/modular/egcd/

題意:

題目要我們找出當p=26513 和 q=32321 時滿足pu+qv=gcd(p,q)時的u和v，而兩者中較小的數值就是flag。

程式碼與簡要註解:

解法一:寫一個gcd的函式

def extended_gcd(a, b):
    # 基本情況：如果 a 為 0，那麼 b 就是 gcd
    # 同時 x 是 0，y 是 1，因為 0 * 0 + b * 1 = b
    if a == 0:
        return b, 0, 1
    else:
        # 遞歸調用 extended_gcd，傳遞參數 (b % a, a)
        gcd, x, y = extended_gcd(b % a, a)
        
        # 返回結果：
        # gcd 為當前的最大公因數
        # x 和 y 是滿足 a * x + b * y = gcd 的係數
        # 更新 x 和 y 的值以適應當前的 a 和 b
        return gcd, y - (b // a) * x, x
      
p = 26513
q = 32321  

# 捕捉 extended_gcd 函數的返回值
gcd, x, y = extended_gcd(p, q)

# print GCD 和最小的係數
print(min(x, y))

＞-8404

這部分的程式碼較為複雜，涉及到了遞迴和回溯的概念

• 遞迴：函數自己呼叫自己，解決子問題。
• 回溯：當遞迴達到基礎情況後，開始逐步返回，每一層的結果都基於下一層的結果進行計算。

以下是我讓chatbot具體的列出了當 a=54, b=16 時，該程式碼每一步驟的數據變化。

具體步驟

• 假設最初調用為 extended_gcd(54, 16)：

  • 第一層遞迴：調用 extended_gcd(16, 54)
  • 第二層遞迴：調用 extended_gcd(6, 16)
  • 第三層遞迴：調用 extended_gcd(4, 6)
  • 第四層遞迴：調用 extended_gcd(2, 4)
  • 第五層遞迴：調用 extended_gcd(0, 2)，這時達到基礎情況，返回 (2, 0, 1)。

• 基礎情況：

  • 在擴展歐幾里得算法中，當 a 等於 0 時，返回 b 作為最大公因數 (GCD)，並返回 x = 0 和 y = 1 作為初始係數。
  • 這時遞迴停止深入，開始回溯。

• 回溯開始：

  • 回溯從最內層的遞迴結束點（基礎情況）開始，逐步返回到最外層的初始調用。

  • 每一層的計算依賴於下一層遞迴調用的結果。

  • 函數在每一層會使用下一層返回的 x 和 y 值來更新當前層的 x 和 y 值，然後返回給上層。

  • 第五層回溯：返回到第四層，計算新的 x 和 y，返回 (2, 1, 0)。

  • 第四層回溯：返回到第三層，計算新的 x 和 y，返回 (2, -1, 1)。

  • 第三層回溯：返回到第二層，計算新的 x 和 y，返回 (2, 3, -1)。

  • 第二層回溯：返回到第一層，計算新的 x 和 y，返回 (2, -10, 3)。

• 回溯完成：當回溯到最初的 extended_gcd(54, 16) 時，整個過程結束，最終結果被返回。

程式如何判斷自動回溯完成的呢？

• 最外層的返回：當函數返回到最外層調用時，回溯過程就完成了。
• 程式結構的特性：遞迴函數的結構是層層嵌套的，每一層調用都等到內部調用完成後才會返回結果。因此，當最外層的計算完成時，所有內部調用也都已經完成。

​
解法二:直接套函示庫

from egcd import egcd
p = 26513
q = 32321  
# 捕捉 extended_gcd 函數的返回值
gcd, x, y = extended_gcd(p, q)

# print GCD 和最小的係數
print(min(x, y))

＞-8404

參考資料:

gcd:

• https://zh.wikipedia.org/zh-tw/%E6%9C%80%E5%A4%A7%E5%85%AC%E5%9B%A0%E6%95%B8#%E8%AE%A1%E7%AE%97
• https://zh.wikipedia.org/wiki/%E8%BC%BE%E8%BD%89%E7%9B%B8%E9%99%A4%E6%B3%95
  egcd:
• https://ccjou.wordpress.com/2012/11/16/%E5%88%A9%E7%94%A8%E5%9F%BA%E6%9C%AC%E5%88%97%E9%81%8B%E7%AE%97%E5%AF%A6%E7%8F%BE%E6%93%B4%E5%B1%95%E6%AD%90%E5%B9%BE%E9%87%8C%E5%BE%97%E6%BC%94%E7%AE%97%E6%B3%95/
• https://ithelp.ithome.com.tw/articles/10320272
• https://hackmd.io/@Koios/rJ_lER719
• chatbot

後話:

今天了解了gcd和egcd，也自己手算推演運算過程。